314 Digits of Pi (Python to Clojure)

Pi Day (3/14) is in a couple of days so I want to wish everyone a Happy Pi Day 2020! It's great to see that 55% of American's plan to celebrate and many will be eating pie or pi-themed food (whatever that is).

My work colleague and basketball buddy Stan sells a nerd t-shirt here: 314 Digits of Pi.py. It has the Python code on the front and the results on the back. I "won" one of these at our annual White Elephant gift exchange in December. Even though the Amazon Best Sellers Rank is #12,306,667 in Clothing, Shoes & Jewelry, I really like it!

I've been staring at the code backward in the mirror for a number of months:

This got me wondering what this algorithm would look like in Clojure?

The first pass on the port was pretty straight forward, but I think it's worth noting some of the subtle differences. All of the code is here: pi-digits.

Here's the original Python code and result:

import math

def pi():
  r = 4*(4*arccot(5) - arccot(239))
  return str(r)[0] + '.' + str(r)[1:-5]

def arccot(x):
  total = power = 10**319 // x
  divisor = 1
  while abs(power) >= divisor:
    power = -power // x**2
    divisor += 2
    total += power // divisor
  return total

print("314 digits of Pi " + pi())

import math

def pi():

r = 4*(4*arccot(5) - arccot(239))

return str(r)[0] + '.' + str(r)[1:-5]

def arccot(x):

total = power = 10**319 // x

divisor = 1

while abs(power) >= divisor:

power = -power // x**2

divisor += 2

total += power // divisor

return total

print("314 digits of Pi " + pi())

$ python3 pi.py
314 digits of Pi 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631

$ python3 pi.py

314 digits of Pi 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631

For the interested, here's an explanation of the calculation of Pi using fixed point math for speed improvements: Pi - Machin: The Machin formula, developed by John Machin in 1706 (!), is:

And here's a Clojure version that returns the identical result:

(ns pi-digits.core
  (:gen-class)
  (:require [clojure.math.numeric-tower :as math]))

(defn pow [b e] (math/expt b e))
(defn abs [n] (math/abs n))

(defn arccot
  [x]
  (let [power (atom (quot (pow 10 319) x))
        total (atom @power)
        divisor (atom 1)]
    (while (>= (abs @power) @divisor)
      (do
        (swap! power #(quot (- %) (pow x 2)))
        (swap! divisor #(+ % 2))
        (swap! total #(+ % (quot @power @divisor)))))
    @total))

(defn pi
  "Calculate Pi to 314 digits"
  []
  (let [r (str (* 4 (- (* 4 (arccot 5)) (arccot 239))))]
    (str (subs r 0 1) "." (subs r 1 315))))

(defn -main
  [& _]
  (println "314 digits of Pi" (pi)))

(ns pi-digits.core

(:gen-class)

(:require [clojure.math.numeric-tower :as math]))

(defn pow [b e] (math/expt b e))

(defn abs [n] (math/abs n))

(defn arccot

[x]

(let [power (atom (quot (pow 10 319) x))

total (atom @power)

divisor (atom 1)]

(while (>= (abs @power) @divisor)

(do

(swap! power #(quot (- %) (pow x 2)))

(swap! divisor #(+ % 2))

(swap! total #(+ % (quot @power @divisor)))))

@total))

(defn pi

"Calculate Pi to 314 digits"

[]

(let [r (str (* 4 (- (* 4 (arccot 5)) (arccot 239))))]

(str (subs r 0 1) "." (subs r 1 315))))

(defn -main

[& _]

(println "314 digits of Pi" (pi)))

One thing I discovered is Python's use of an arbitrary-precision integer implementation that allows 10³¹⁹to actually have 319 digits of precision. The use of Java's double power implementation, (Math/pow b e) in Clojure, will not work because a double value can only represent about ± 10³⁰⁸. Getting the required precision required the use of the clojure/math.numeric-tower library and the (math/expt b e) function (integer implementation when e is a positive value).
The Clojure quot[ient] does the same thing as Python's floor division (//) function.

One problem with the arccot (arc-cotangent) implementation is that it just duplicates the Python logic and is not idiomatic Clojure. Instead of coding this in a non-functional style, i.e. using mutable state (atom), let's create a functional version:

(defn arccot-recur
  [x]
  (loop [power (quot (pow 10 319) x)
         divisor  1
         tot 0]
    (let [total (+ tot (quot power divisor))]
      (if (>= (abs power) divisor)
        (recur (quot (- power) (pow x 2)) (+ divisor 2) total)
        total))))

(defn arccot-recur

[x]

(loop [power (quot (pow 10 319) x)

divisor 1

tot 0]

(let [total (+ tot (quot power divisor))]

(if (>= (abs power) divisor)

(recur (quot (- power) (pow x 2)) (+ divisor 2) total)

total))))

We use loop/recur for a recursive implementation. This has the benefit of tail-call optimization (TCO). Here are the execution times (average of 10 runs) for calculating Pi with the three implementations:

Method	Digits Time in seconds
	10,000	50,000	100,000	200,000
python	0.158	3.74	14.9	60.3
clojure-while	0.260	5.14	19.8	78.6
clojure-recur	0.252	5.10	19.8	78.5

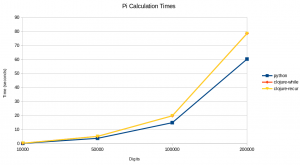
Python is certainly faster, but the purpose here was not to compare computation speed. It was to get a Clojure version of the t-shirt made! Who's the real nerd now? 🙂

Leave a Reply

Recent Posts

Categories

Archives

Blogroll

Sites I Visit

Meta

Twitter Updates